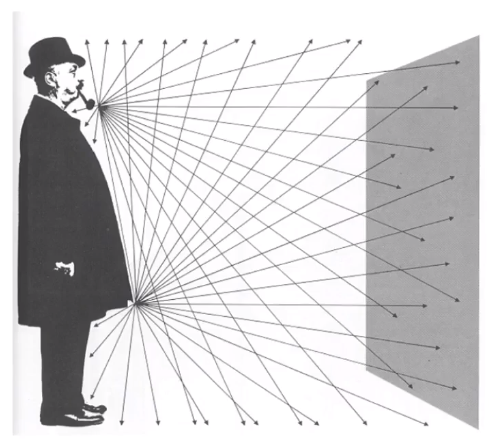
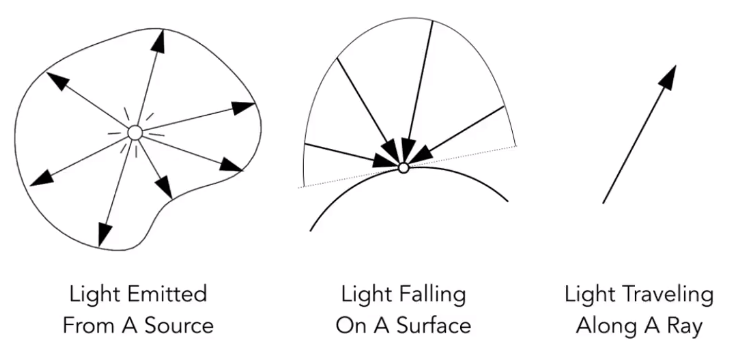
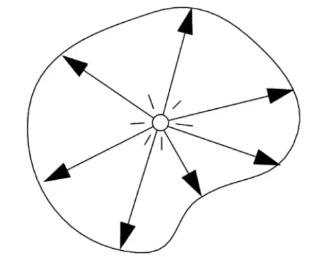
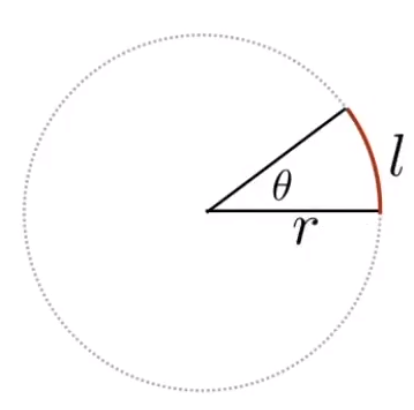
以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# 辐射度量学(Basic radiometry)
主要是用来定义光的一些空间中的属性。
- 辐射通量(Radiant flux)
- 强度(Radiant Intensity)
- 照度(Irradiance)
- 亮度(Radiance)
# Radiant Energy and Flux(Power)
# 辐射能量(Radiant Energy)
光线自身的能量,单位 J —— 焦耳。
Q[J=Joule]
# 辐射功率(Radiant Flux)
单位时间的能量(功率),单位 W —— 瓦特 or lm —— 流明。
Φ=dtdQ[W=Watt][lm=lumen]∗
「Flux」也可以理解为,单位时间内,通过传感器的光子数量。
![image-20210122144910546]()
# Other Important Light Measurements
- 从光源可以辐射出的能量。(Radiant Intensity)
- 每个物体的表面能够接收到的能量。(Irradiance)
- 光线传播中的能量。(Radiance)
![image-20210122145137496]()
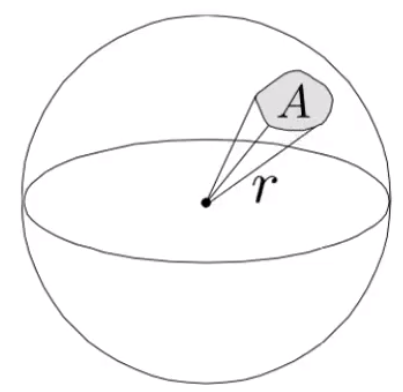
# 辐射强度(Radiant Intensity)
辐射强度是指点光源发出单位「立体角(solid angle)」的功率。
![image-20210122152517696]()
I(ω)=dωdΦ
[srW][srlm=cd=candela]
# What is 「solid angle」❓
# Angles and Solid Angles
角度的定义:
- 弧度:θ=rl 。
- 圆的弧度(radians)是 2π。
![image-20210122165235939]()
立体角的定义:
- 投影面积:Ω=r2A 。
- 球的立体度(steradians)为 4π。
![image-20210122165524771]()
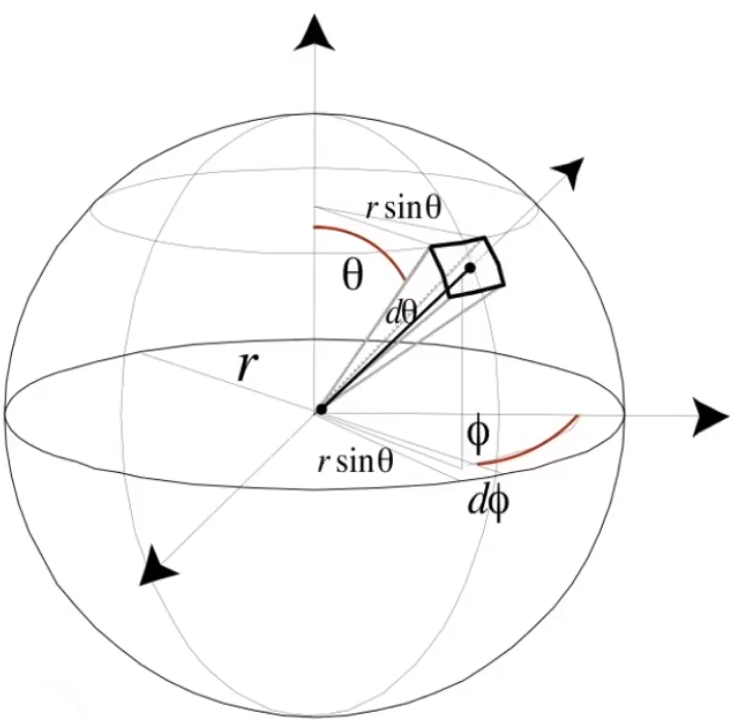
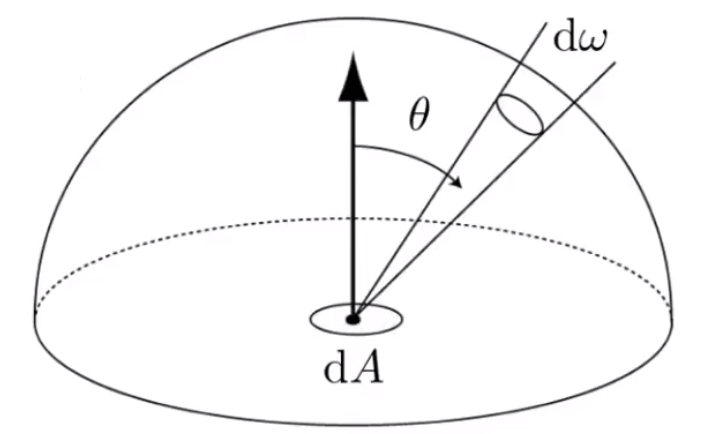
# 微分立体角(Differential Solid Angles)
对 x,y 两个轴的偏角为 θ,ϕ。要求的投影的面积,可以理解为对一个二维的坐标求积分。
假设沿着垂直方向偏移 dθ 个单位的弧度,沿着水平方向便宜 dϕ ,已知球的半径为 r,根据 弧长=弧度×半径 。
可以求得投影的长和宽分别是 rdθ 和 rsinθdϕ 。由此,便可以计算出矩形的面积 dA。
![image-20210122170057325]()
已知在 x,y 的角度分为别 θ,ϕ,计算面积的公式如下:
dA=(rdθ)(rsinθdϕ)=r2sinθdθdϕ
通过计算到的面积,就可以求得「微分立体角」:
Ω=r2A→dω=r2dA=sinθdθdϕ
对于整个球来说,把所有方向的「微分立体角」求积分,就可以得到球的「立体度」:
Sphere: S2Ω=∫S2dω=∫02π∫0πsinθdθdϕ=4π
相关扩展阅读:传送门
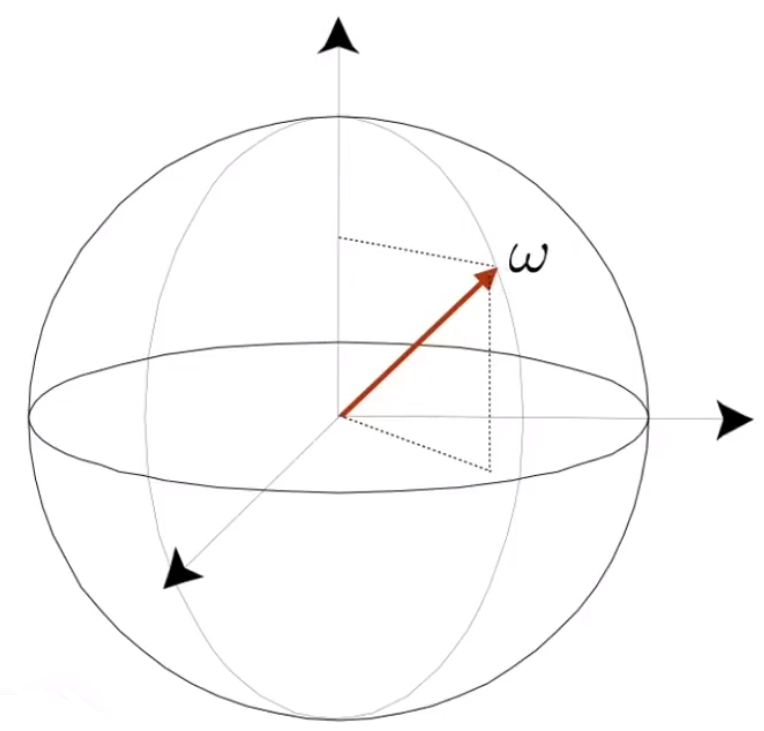
# 通过 ω 定义一个微分立体角
空间中的向量,一版可以用 ω 表示, ω 又可以通过 θ,ϕ 的方式定义其位置和方向。(单位长度)
![image-20210122173720738]()
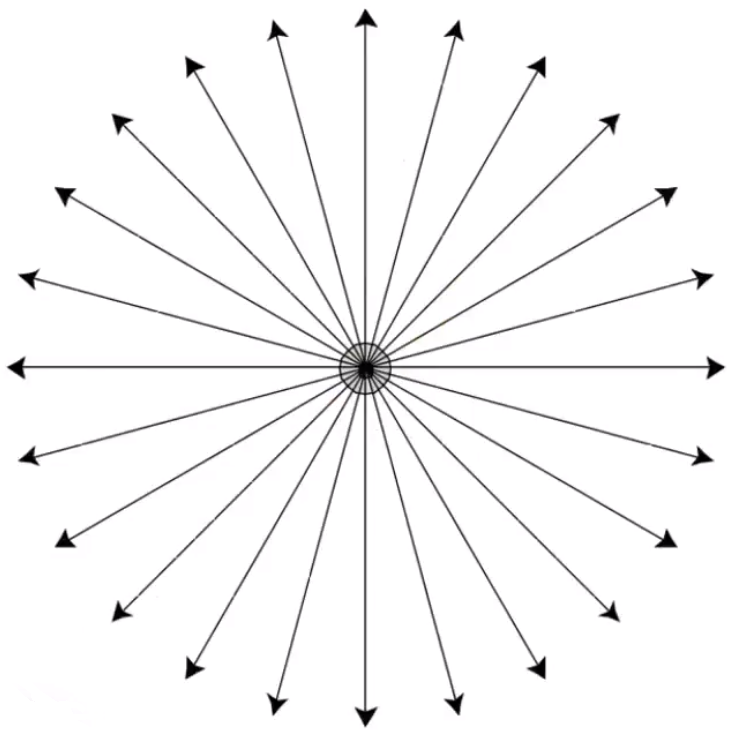
# Isotropic Point Source
一个点光源的辐射可以视作一个球体。已知球体的立体度为 4π。那么在某个单位向量的光线强度 I 就等于总能量除以球体的立体度4πΦ。
![image-20210122174129463]()
Φ=∫S2Idω=4πI→I=4πΦ
# 照度(Irradiance)
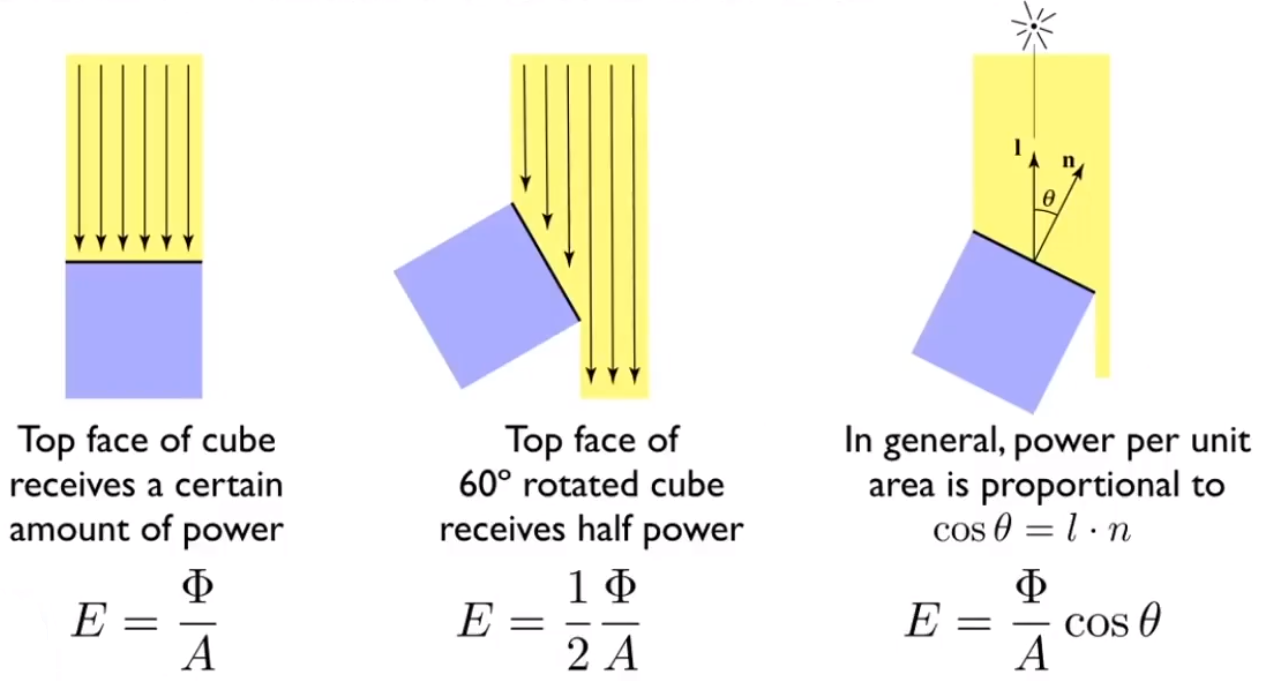
照度其实就是用来表示单位面积的「入射光照」功率。
![image-20210124145012305]()
E(x)=dAdΦ(x)[m2W]=[m2lm=lux]
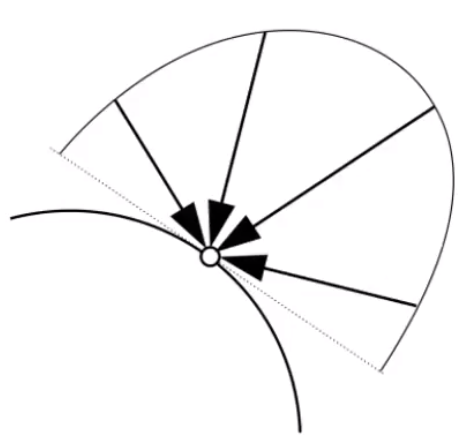
此处定义的入射光照,必须是垂直于物体表面的光线。如果光线和物体表面不垂直,则必须转换成垂直的光线。
所以不同角度的入射光线,会影响每个点所接受到的「Irradiance」值。
![image-20210124145452051]()
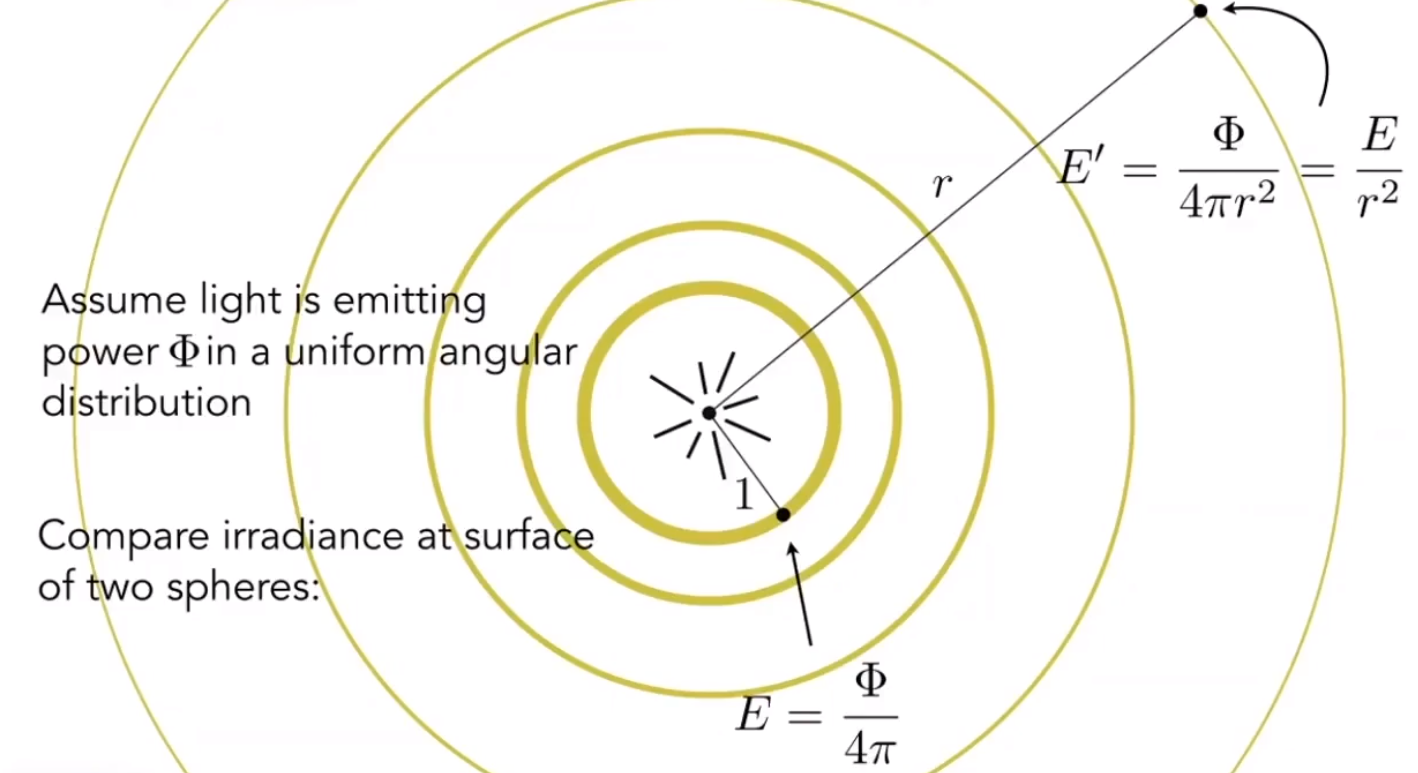
同样,光线的「Irradiance」还会根据传播的距离进行衰减,由于辐射范围越大,导致辐射到的球面积越大,最终使得每个辐射点的「Irradiance」越小。
![image-20210124145823255]()
# 亮度(Radiance)
单位面积的区域内「接受」的入射光线,所辐射到单位立体角上的功率。
Irradiance:单位面积内接受到的射入光功率。
Instensity:物体辐射光线到单位立体角的功率。
Radiance:「Irradiance」的功率,辐射到单位立体角内的数值;或者「Instensity」辐射出的功率,所需单位面积接受到多少的功率。
![image-20210124150532452]()
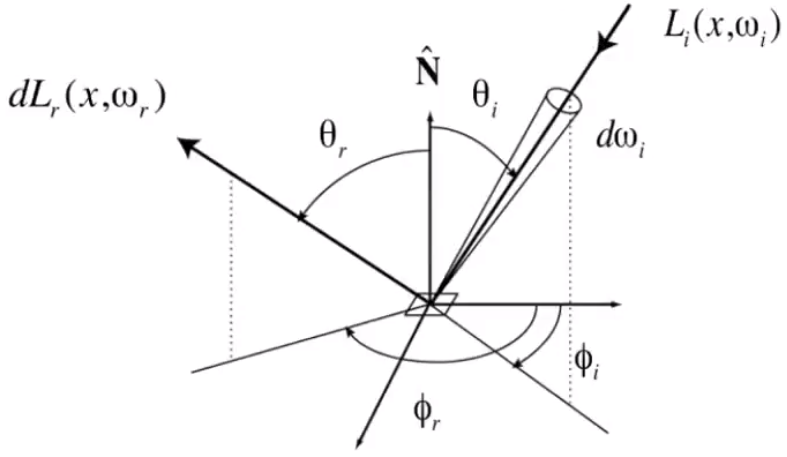
L(p,w)=dwdAcosθd2Φ(p,w)[m2srW][m2cd=m2srlm=nit]
# 入射亮度(Incident Radiance)
表示从单位立体角射入的照度(Irradiance)。
![image-20210124151905413]()
L(p,w)=dwcosθdE(p)
# 出射亮度(Exiting Radiance)
表示从单位面积辐射出的辐射强度(Intensity)
![image-20210124152530251]()
L(p,w)=dAcosθdI(p,w)
# Irradiance vs Radiance
- Irradiance:表示一个单位面积收到的总功率 x。
- Radiance:总功率为 x 的光线,从某个立体角射入,所能给单位面积接受到的总功率 x′ 。
![image-20210124153658949]()
dE(p,w)=Li(p,w)cosθdw
单位面积接受到的总功率,可以理解为对半球表面每个单位面积求和,即:对单位半球面积上的每个入射光求积分。
单位半球面积:H2→E(p)=∫H2Li(p,w)cosθdw
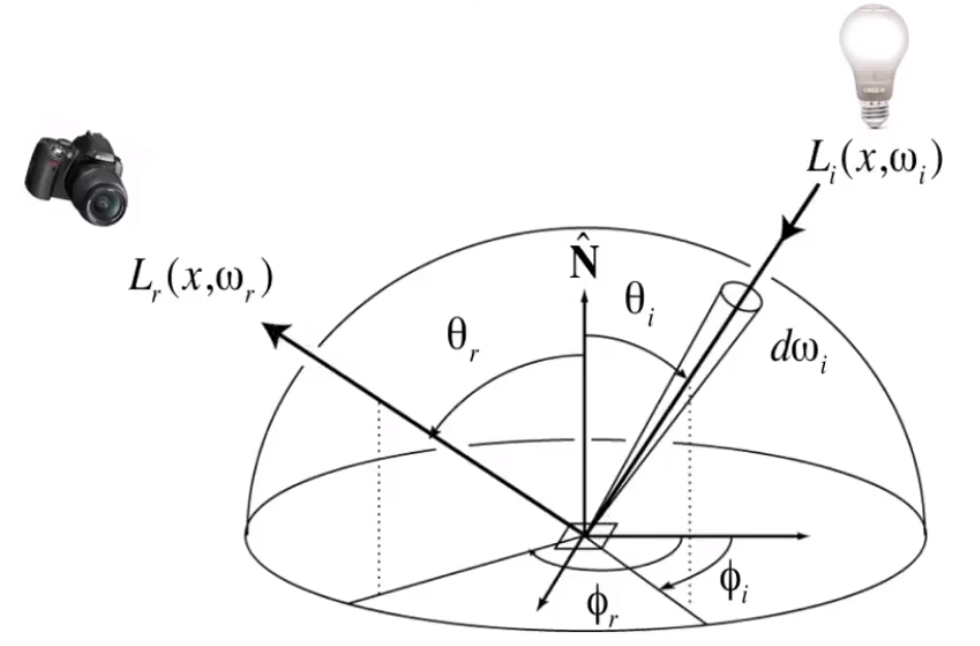
# 双向反射分布函数(Bidirectional Reflectance Distribution Function)——BRDF
用于描述从一个方向射入的光线,反射到各个方向上的能量值。
或者理解成,一个物体吸收了某个方向射入的光线,辐射到各个方向的光线功率。
通常也可以理解为物体本身的材质(materials)属性。
如下图:
- 从 wi 立体角方向射入的光线。
- 照射到物体表面单位面积 dA 。
- 并把能量辐射到立体角方向为 wr 。
![image-20210124154637935]()
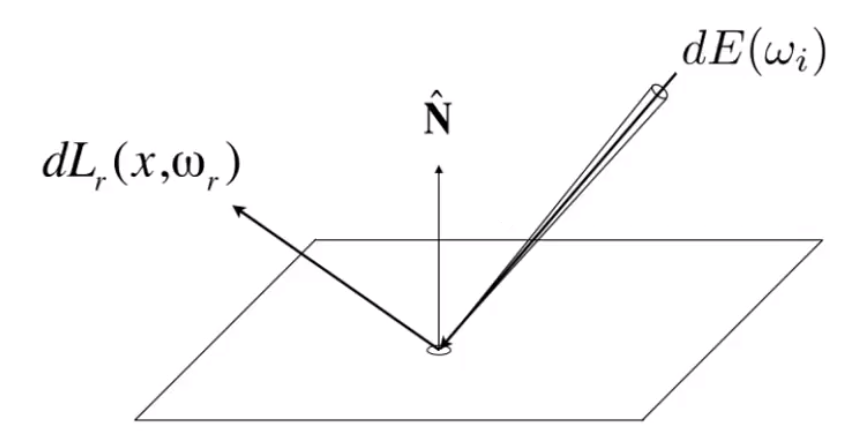
A点接受到的能量:dE(wi)=L(wi)cosθidwi
# 如何把 dE(wi) 转变为 dLr(x,wr) ❓
通过 BRDF 计算辐射出的能量。这里假定是漫反射,那么每个单位的能量就是球面度分之一 sr1 。
![image-20210124155523168]()
fr(wi→wr)=dEi(wi)dLr(wr)=Li(wi)cosθidwidLr(wr)[sr1]
# Light Transport
# 反射方程(The Reflection Equation)
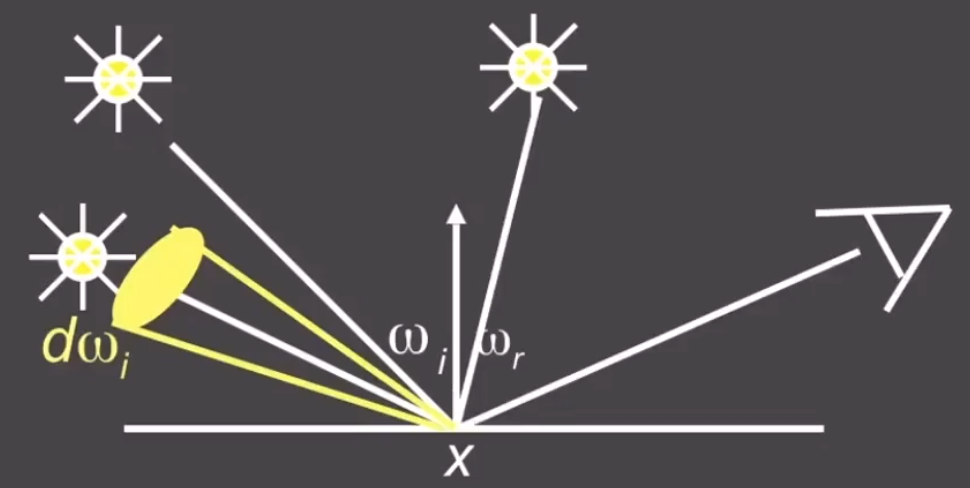
现在已知一个方向的入射光反射到另一个方向上的功率,那么就可以通过积分每个方向的入射光到该方向上的功率,得到该点观察时的「总功率」。
![image-20210124162341830]()
Lr(r,wr)=∫H2fr(p,wi→wr)Li(p,wi)cosθidwi
# 渲染方程(The Rendering Equation)
把物体自身的发光值加上对其他物体的反射光值,就是最终的渲染方程。
这里的球面,认为负半球不透光,cosθ=n⋅wi ,且 cosθ>0
Lo(p,wo)=Le(p,wo)+∫Ω+Li(p,wi)fr(p,wi,wo)(n⋅wi)dwi
# 积分方程(Integral Equation)
![image-20210126202227908]()
渲染方程:Lr(x,wr)=Le(x,wr)+∫ΩLr(x′,−wi)f(x,wi,wr)cosθidwi
其中各个部分含义如下:
Lr(x,wr):物体最终的光照,未知,需要计算。
Le(x,wr):物体自身的光照,已知。
∫ΩLr(x′,−wi):物体的反射光,未知。
f(x,wi,wr)cosθidwi:光线反射系数,BRDF,入射角余弦, 已知。
简化后的方程式,u 表示观察物体,v 表示其他光源:
l(u)=e(u)+∫l(v)K(u,v)dv
简化成算子形式,L 观察值,E 观察物体自身光照,KL 其他物体发出并被观察物体反射的光照
L=E+KL
# 方程展开
L=E+KL
L−KL=E
(1−K)L=E
L=(1−K)−1E
二项式定理:
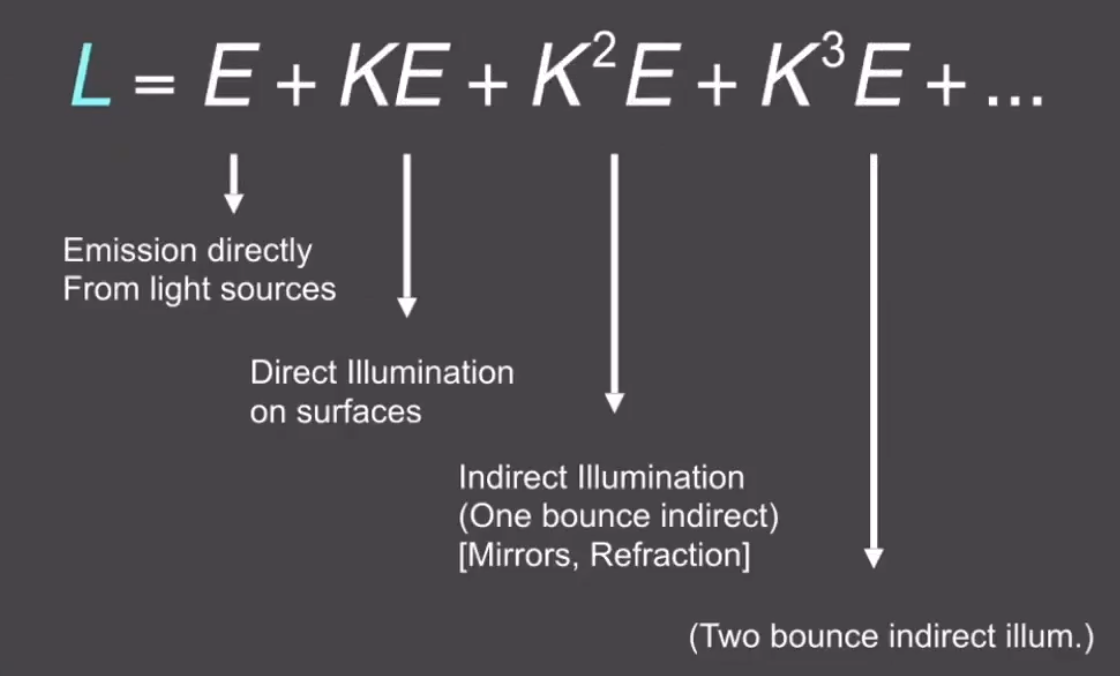
L=(1+K+K2+K3+...)E
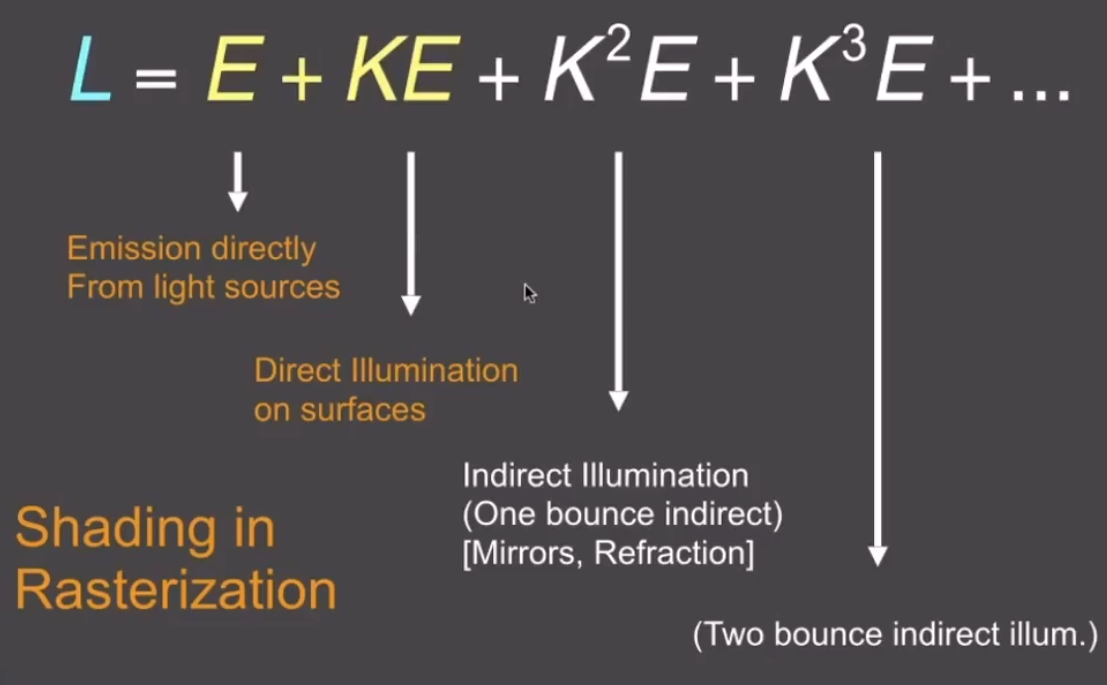
L=E+KE+K2E+K3E+...
![image-20210126204247094]()
光栅化的渲染模式,只能够比较准确的处理物体自己的光照,和经过物体弹射一次的光照。再多的弹射次数下,性能要求指数增长。
![image-20210126213243692]()
# 关键字
- 泰勒级数 —— 几何级数:1−x1=∑n=0∞xn=1+x2+x3+...+xn∀x:∣x∣<1
- 全局光照(Global illumination):直接光照(物体自身辐射光照)+ 间接光照(物体反射其他光源的光照)