以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# Linear Algebra
# 向量(Vectors)
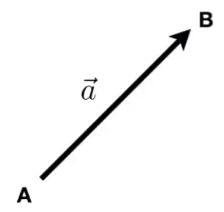
# 向量的表示:
![image-20201227124153407]()
AB=B−A=a
# 向量的属性:
- 方向: A -> B。表示由 A 点到 B 点的方向。
- 长度:∣∣a∣∣。表示 A 点和 B 点的距离。
# 单位向量(normalize):
长度为 1 的向量被称为单位向量。
a^=∣∣a∣∣a
# 向量基本操作
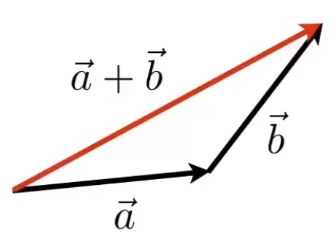
# 向量求和
![image-20201227131157472]()
# 笛卡尔坐标下(Cartesian Coordinates)
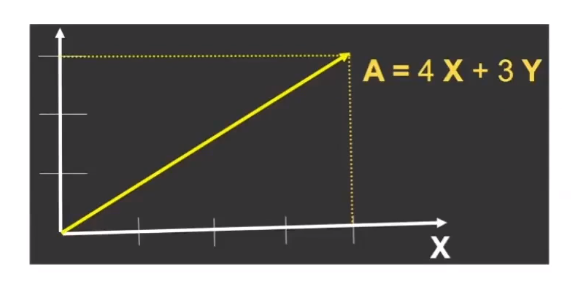
![image-20201227131432836]()
A=(xy)AT=(x,y)∣∣A∣∣=x2+y2
笛卡尔坐标下,向量求和等于对应的元素相加得到的「向量」
a+b=(xaya)+(xbyb)=(xa+xbya+yb)
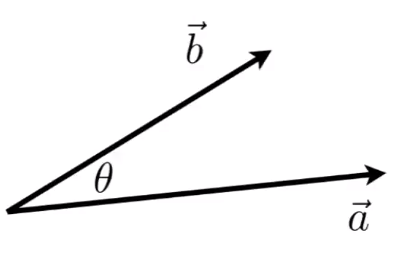
# 点乘(Dot product)—— 「⋅ 」
两个单位向量的点乘表示两个单位向量夹角的 cos 值
![image-20201227133122765]()
a⋅b==∣∣a∣∣∣∣b∣∣cosθ
cosθ=∣∣a∣∣∣∣b∣∣a⋅b→cosθ=a^⋅b^
# 性质:
满足乘法的「交换律」、「分配律」和「结合律」
- a⋅b=b⋅a
- a⋅(b+c)=a⋅b+a⋅c
- ka⋅b=a⋅(kb)=k(a⋅b)
# 笛卡尔坐标下(Cartesian Coordinates)
笛卡尔坐标下「点乘」等于对应的元素相乘并相加得到的「值」
a⋅b=(xaya)⋅(xbyb)=xaxb+yayb
a⋅b=⎝⎛xayaza⎠⎞⋅⎝⎛xbybzb⎠⎞=xaxb+yayb+zazb
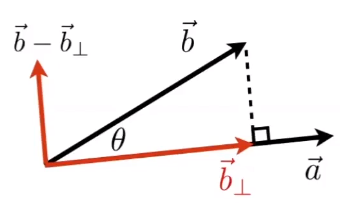
# 向量的投影:
向量 b在 向量 a上的投影,记作向量 b⊥
![image-20201227141947866]()
b⊥=∣∣b⊥∣∣a^
∣∣b⊥∣∣=∣∣b∣∣cosθ
b⊥=(∣∣b∣∣cosθ)a^→b⊥=(b⋅a^)a^
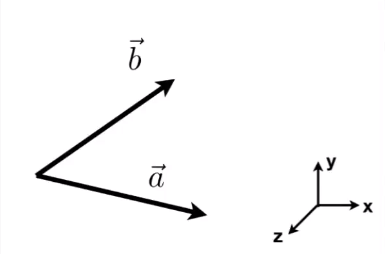
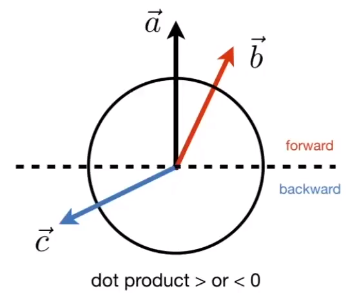
# 判断两个向量是否同向:
两个单位向量的「点乘」结果为 cosθ ,可以表示两向量的方向是否接近
![image-20201227144112844]()
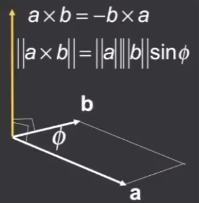
# 叉乘(Cross product)—— 「×」
通过两个向量进行「叉乘」,得到垂直于这两个向量的「新向量」。该向量的方向通过「右手螺旋法则」决定:
例如 a×b那么右手四指从 a 指向 b,大拇指所指方向就是新向量方向。
![image-20201227151139009]()
# 三维空间的直角坐标系建立
- x×y=+z:该情况下,符合右手坐标系
- ∣∣z∣∣=∣∣x∣∣∣∣y∣∣sinθ :叉乘的长度等于两个向量长度乘以 sinθ
- x×x=0:相同向量叉乘结果为 0 向量,因为 sinθ=0
# 符合「分配率」和「结合率」,遵循「逆交换律」
- a×b=−b×a
- a×(b+c)=a×b+a×c
- a×(kb)=k(a×b)
# 代数计算公式:
a×b=⎝⎛xayaza⎠⎞×⎝⎛xbybzb⎠⎞=⎝⎛yazb−ybzazaxb−xazbxayb−yaxb⎠⎞
# 矩阵计算公式( A∗ 表示向量 a的伴随矩阵):
a×b=A∗b=⎝⎛0za−ya−za0xaya−xa0⎠⎞⎝⎛xbybzb⎠⎞
# 叉乘意义:
用于判断统一平面内的两个向量之间的关系
左右关系:
- 左 —— 逆时针方向
- 右 —— 顺时针方向
- 例如下图所示,如果 a×b=+z那么可以认为 b在 a的左侧,反之则反之。
![image-20201227154247745]()
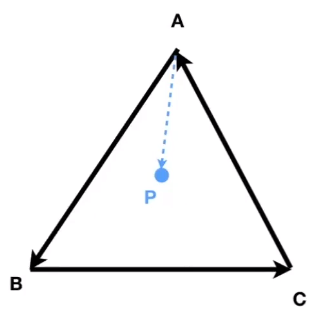
内外关系:
- 内 —— 三角形内部
- 外 —— 三角形外部
- 例如下图所示,分别计算「三条边」和「三个顶点与 P 点形成的向量」的叉乘,如果三个结果是同向(±Z),那么可以判断,点 P 在三角形内部。否则,P 点在三角形外部。
- AB×AP=+Z
- BC×BP=+Z
- CA×CP=+Z
![image-20201227154623986]()
# 向量的其他操作
# 定义一个基本的右手坐标系
∣∣x∣∣=∣∣y∣∣=∣∣z∣∣=1
x⋅y=x⋅z=y⋅z=0
z=x⋅y
# 将某个向量分解成其他的方向向量
p=(p⋅x^)x^+(p⋅y^)y^+(p⋅z^)z^
# 矩阵(Matrices)
# 矩阵运算
# 矩阵乘积
矩阵相乘时,只有「前矩阵的行数」等于「后矩阵的列数」,乘积才有意义。
某个位置的:值 = 「该位置前矩阵所在行」点乘「该位置后矩阵所在列」
⎝⎛150324⎠⎞(32679843)=⎝⎛9198x4428336132132612⎠⎞
矩阵相乘,最终得到的行列数取决于「前矩阵的列」和「后矩阵的行」:(M×N)(N×P)=(M×P)
# 没有任何的「交换律」,但满足「结合律」和「分配律」
AB ≠ BA
(AB)C = A(BC)
A(B+C) = AB +AC
(A+B)C = AC + BC
# 矩阵变换
(−1001)(xy)=(−xy)
# 矩阵转置
- (AB)T=BTAT
⎝⎛150324⎠⎞=(135204)T
# 单位矩阵
I3X3=⎝⎛100010001⎠⎞
# 逆矩阵
AA−1=A−1A=I
(AB)−1=B−1A−1
# 伴随矩阵
A=(acbd),adj(A)=(dc−ba)
用的不多,具体细节见 wiki: 传送门
# 矩阵形式的向量乘法
a⋅b=aTb=⎝⎛xayaza⎠⎞(xbybzb)=(xaxb+yayb+zazb)
- 叉乘( A∗ 表示向量 a的伴随矩阵)
a×b=A∗b=⎝⎛0za−ya−za0xaya−xa0⎠⎞⎝⎛xbybzb⎠⎞=⎝⎛yazb−ybzazaxb−xazbxayb−yaxb⎠⎞
# 关键字
![image-20201227154247745]()
![image-20201227154623986]()