# Transformation

# 常见的 2D 矩阵变换（2D Transforms）

# 大小变换（Scale）

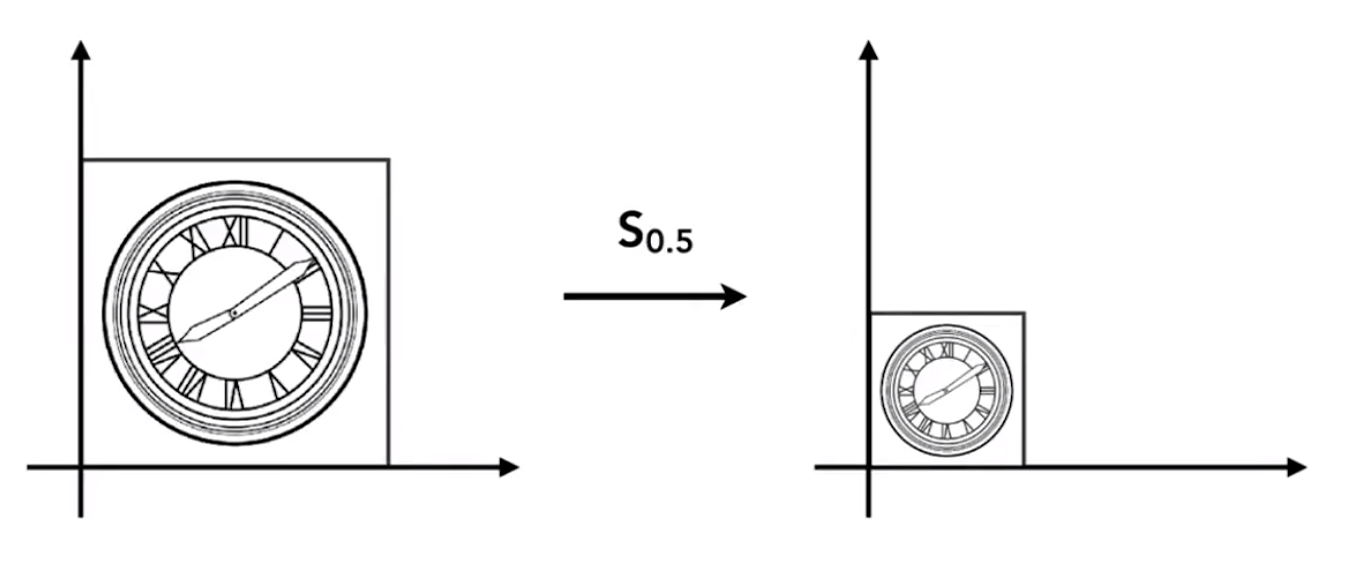
各个坐标放大或者缩小

$$\text{缩放矩阵:} \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} \quad \to \quad \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix}$$

# 翻转（Reflection）

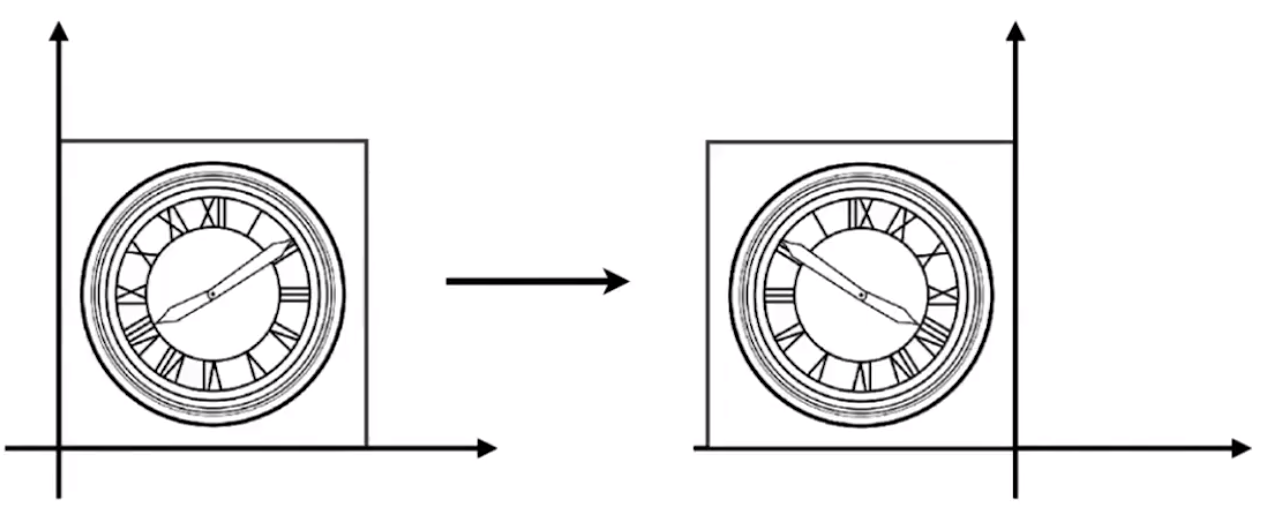
各个坐标取反

$$\text{翻转矩阵:} \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \quad \to \quad \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix}$$

# 切变（Shear）

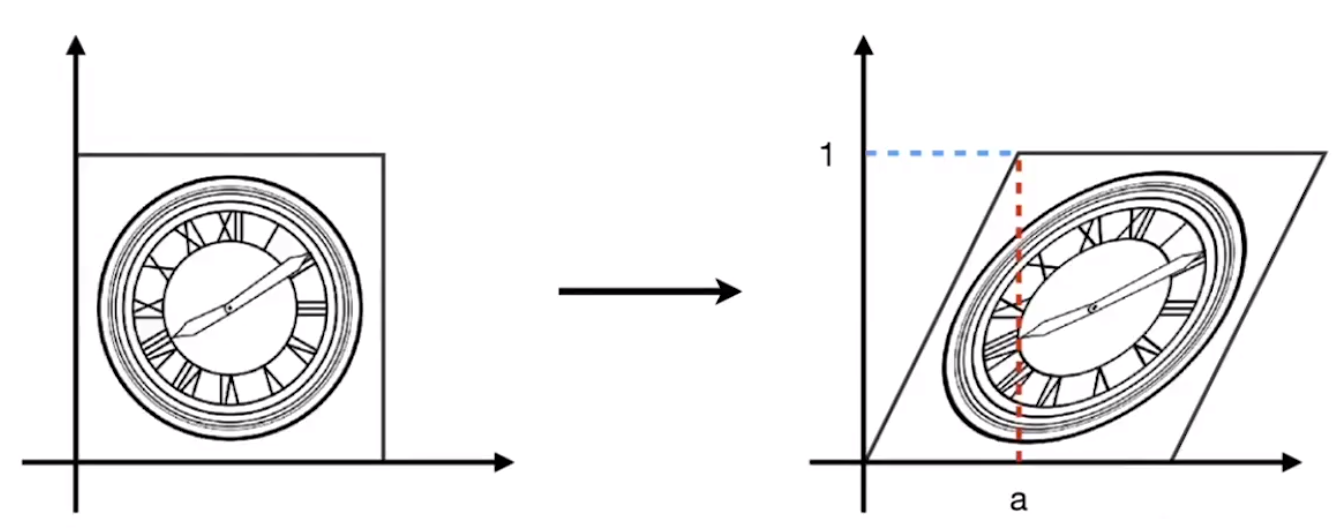
y 坐标不变，x 坐标水平移动，移动距离取决于矩阵右上角的值（ay）

$$\text{切变矩阵:} \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \quad \to \quad \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x + ay \\ y \end{bmatrix} = \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix}$$

# 旋转（Rotate）

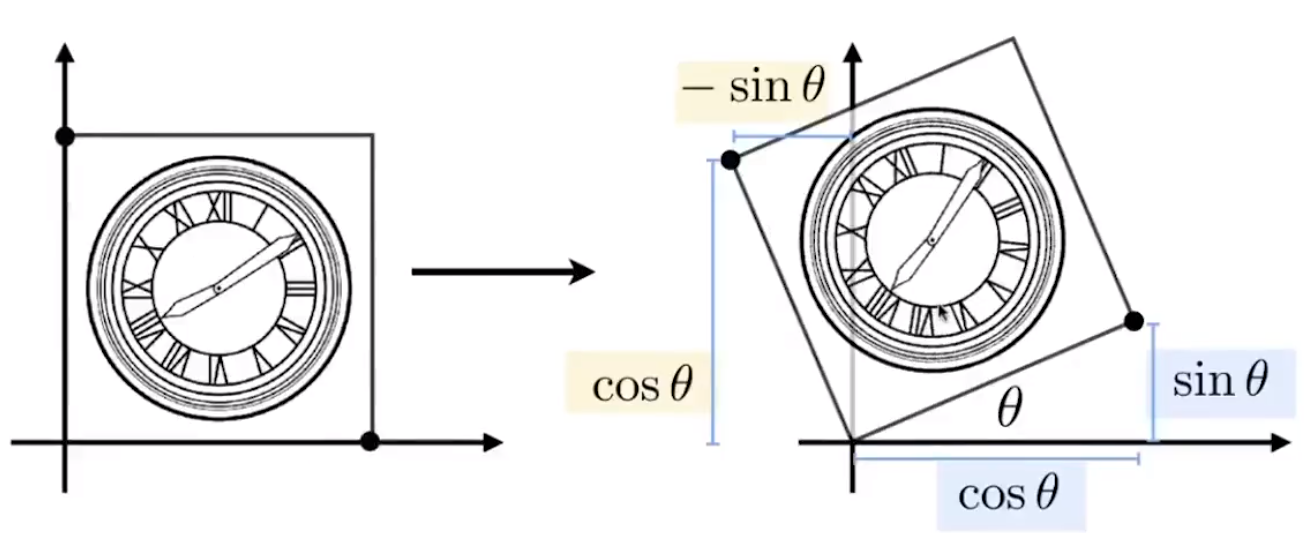
默认情况下，绕着原点（0，0）逆时针进行旋转

$$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} - \sin \theta \\ \cos \theta \end{bmatrix} \quad \to \quad b = - \sin \theta \quad, d = \cos \theta$$

$$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \cos \theta \\ \sin \theta \end{bmatrix} \quad \to \quad a = \cos \theta \quad, c = \sin \theta$$

$$\text{旋转矩阵:} \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}$$

# 线性变换规则（Linear Transforms）

任何一个坐标，如果可以通过一个矩阵进行变换得到，那么称之为「线性变换」

$$x^{\prime} = Mx \quad \to \quad \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$$

$$x^{\prime} = ax + by$$

$$y^{\prime} = cx + dy$$

# 齐次坐标（Homogeneous coordinates）

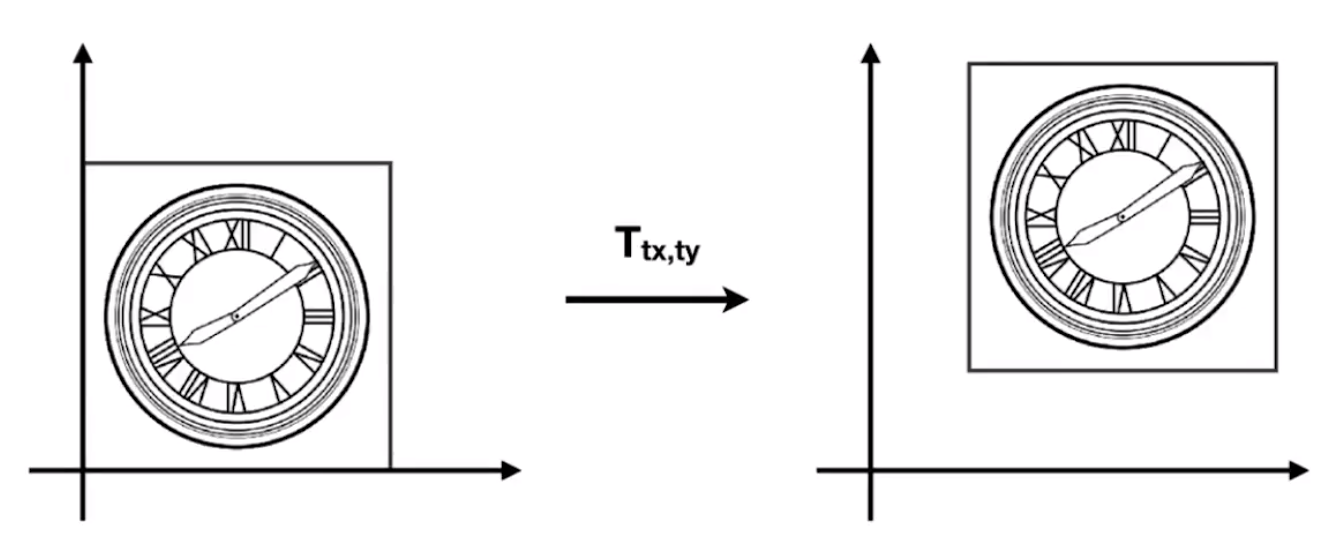
引入「齐次坐标」的目的，是为了解决「平移矩阵」，常规的平移，没用办法通过「线性变换」得到

$$x^{\prime} = x + t_x$$

$$y^{\prime} = y + t_y$$

$$\begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_{x} \\ t_{y} \end{bmatrix}$$

$t_x$ 和 $t_y$ 没办法通过 $ax + by$ 的形式得到，它是一个固定值

# 新增一个 w 坐标维度

为了能够实现平移的效果，又可以让整体计算变得统一，所以引入了一个新的 w 坐标维度。

• 2D 平面内的向量： $(x,y,0)^T$。
• 2D 平面内的点：$(x,y,1)^T$

# 为什么向量的齐次坐标是 $(x,y,0)^T$

• vector + vector = vector
• point - point = vector
• point + vector = point
• point + point = point（这两个点的中点）

向量的第三维是 0，是为了保证平移操作不会影响向量本身的方向和值。

# 为什么点的其次坐标是$(x,y,1)^T$

其实也可以非 1，但是最终都可以转换成为 1 的情况。只要 w 不为 0（为 0 的情况下视作向量）

# 齐次坐标下的平移操作

$$\begin{pmatrix} x^{\prime} \\ y^{\prime} \\ w^{\prime} \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x + t_x \\ y + t_y \\ 1 \end{pmatrix}$$

# 齐次坐标下的其他操作：

任何仿射变换（Affine Transformations）都可以转换成 齐次坐标变换

$$\text{仿射变换：} \begin{pmatrix} x^{\prime} \\ y^{\prime} \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix}$$

$$\text{齐次坐标变换:} \begin{pmatrix} x^{\prime} \\ y^{\prime} \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$$

注意，所有的变换都是先处理线性变换 $\cdot (x,y)^T$，再处理平移 $+ (t_x,t_y)^T$

# Scale

$$\text{缩放:} \quad S_{(s_x,s_y)} = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

# Rotation

$$\text{旋转:} \quad R_{(\alpha)} = \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

$$\text{旋转:} \quad R_{(-\alpha)} = \begin{pmatrix} \cos \alpha & \sin \alpha & 0 \\ -\sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

$${R_{(\alpha)}}^T = R_{(-\alpha)}$$

# Translation

$$\text{平移:} \quad T_{(t_x, t_y)} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix}$$

# 多次变换的情况下：

操作顺序从右到左依次进行。

$$\text{先旋转45度后,再平移1个单位:} \quad T_{(1,0)} \cdot R_{45} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} cos45^{\circ} & -sin45^{\circ} & 0 \\ sin45^{\circ} & cos45^{\circ} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$$

# 如何围绕某个点进行旋转？

可以看成是先对图像进行平移，在进行旋转，再进行平移

$$T_{(c)} \cdot R_{(\alpha)} \cdot T_{(-c)}$$

# 关键字

• 仿射变换（Affine Transformations）：线性变换 （缩放，旋转，翻转、切变）+ 平移

• 正交矩阵：矩阵 = 矩阵的逆 R_{- \theta} = {R_{\theta}}^