以下为个人学习笔记整理,涉及坐标内容统一用右手坐标系,课程官网。
# 三维空间下的向量和点
3D vector = (x,y,z,0)T
3D point = (x,y,z,1)T
向量和点的定义和二维空间类似。
# 三维空间下的齐次坐标矩阵
⎝⎜⎜⎜⎛x′y′z′1⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛adg0beh0cfi0txtytz1⎠⎟⎟⎟⎞⋅⎝⎜⎜⎜⎛xyz1⎠⎟⎟⎟⎞
# Scale
S(sx,sy,sz)=⎝⎜⎜⎜⎛sx0000sy0000sz00001⎠⎟⎟⎟⎞
# Translation
T(tx,ty,tz)=⎝⎜⎜⎜⎛100001000010txtytz1⎠⎟⎟⎟⎞
# 绕轴旋转
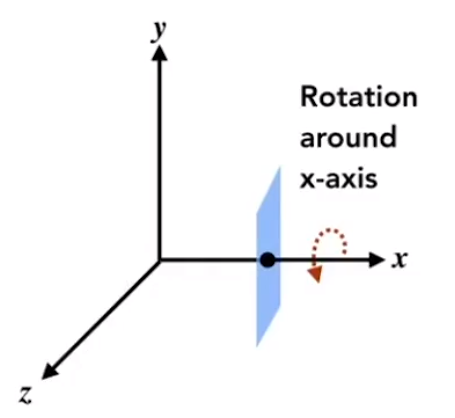
默认情况下都是绕着某个轴,逆时针旋转。
![image-20201228171756050]()
绕 X 轴旋转的情况下,x 坐标是不变的,所以,第一行和第一列不受影响
绕 x 轴 旋转:Rx(α)=⎝⎜⎜⎜⎛10000cosαsinα00−sinαcosα00001⎠⎟⎟⎟⎞
绕 Y 轴旋转的情况下,y 坐标是不变的,所以,第二行和第二列不受影响
绕 y 轴 旋转:Ry(α)=⎝⎜⎜⎜⎛cosα0−sinα00100sinα0cosα00001⎠⎟⎟⎟⎞
绕 Z 轴旋转的情况下,z 坐标是不变的,所以,第三行和第三列不受影响
绕 z 轴 旋转:Rz(α)=⎝⎜⎜⎜⎛cosαsinα00−sinαcosα0000100001⎠⎟⎟⎟⎞
# 为什么 Ry 看起来是反的?
因为 x,y,z 之前的循环对称关系,导致,其中总会有一组坐标的相乘是反向的。
x^×y^=z^
y^×z^=x^
z^×x^=−y^
x^×z^=y^
# 3D 旋转
欧拉角(Euler angles):Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ)
- Model(模型)transformation:把场景的物体摆放好
- View(视图)/ Camera transformation:把摄像机放在一个合适的位置
- Projection(投影)
- Orthographic(正交)
- Perspective(透视)
# 视图📷
- Position: e
- Look-at / gaze direction:g
- Up direction:t
# 观察的关键
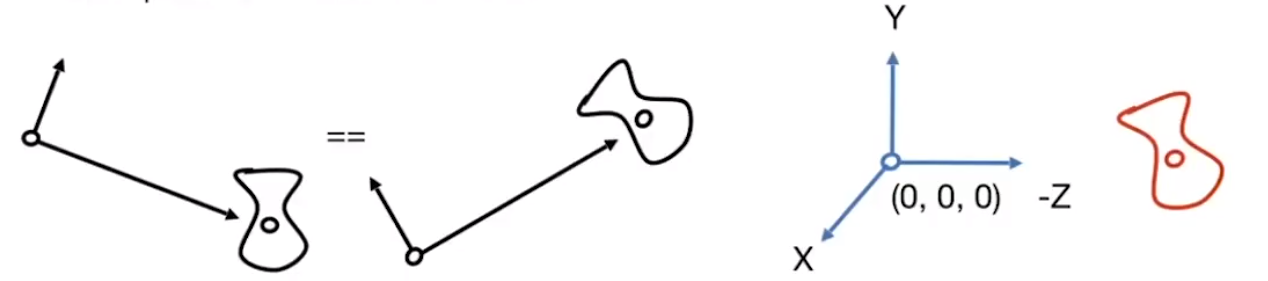
![image-20201228174243349]()
只要保证上述两点,不论何地,最终的画面就不会改变。所以通常情况下,会把相机放在「原点坐标」。
# 如何把相机移动到原点,且 g=−z
Mview=Rview⋅Tview
Tview=⎣⎢⎢⎢⎡100001000010−xe−ye−ze1⎦⎥⎥⎥⎤
假设:Mview=⎣⎢⎡xg×tyg×tzg×txtytztx−gy−gz−g⎦⎥⎤
x^view=⎣⎢⎢⎢⎡xg×tyg×tzg×t0⎦⎥⎥⎥⎤,y^view=⎣⎢⎢⎢⎡xtytzt0⎦⎥⎥⎥⎤,z^view=⎣⎢⎢⎢⎡x−gy−gz−g0⎦⎥⎥⎥⎤
- 如何把正常的坐标向量转化为 Mview 的坐标向量呢?
正常的坐标矩阵:Mnormal=⎣⎢⎡100010001⎦⎥⎤
x^normal=⎣⎢⎢⎢⎡1000⎦⎥⎥⎥⎤,y^normal=⎣⎢⎢⎢⎡0100⎦⎥⎥⎥⎤,z^normal=⎣⎢⎢⎢⎡0010⎦⎥⎥⎥⎤
R⋅x^normal=x^view,R⋅y^normal=y^view,R⋅z^normal=z^view
- 通过上述公式,可以把 R 的矩阵求出来。那么从正常坐标向量变换到摄像机的坐标向量的矩阵就可以求得(Rview−1)
Rview−1=⎣⎢⎢⎢⎡xg×tyg×tzg×t0xtytzt0x−gy−gz−g00001⎦⎥⎥⎥⎤
- 然后再对 Rview−1 取逆矩阵,就可以得到,从摄像机坐标变换到正常世界坐标的矩阵(Rview)
Rview=⎣⎢⎢⎢⎡xg×txtx−g0yg×tyty−g0zg×tztz−g00001⎦⎥⎥⎥⎤
# Projection📽
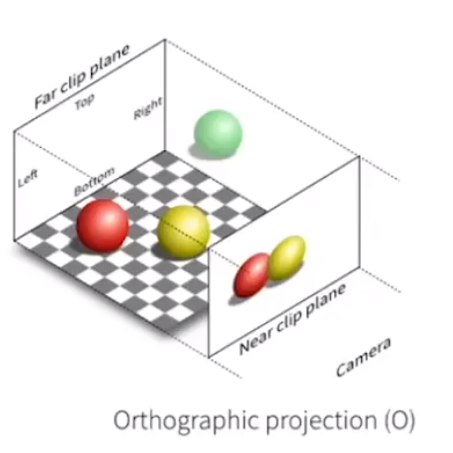
# 正交(Orthographic)投影
![image-20201228212823621]()
- 相机 lookat: −z,up:y
![image-20201231112436972]()
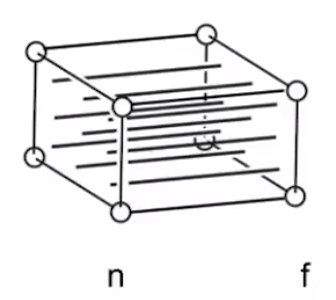
# 正交投影也可以被看作是一个立方体:
![image-20201231155824631]()
# 一般情况下正则化(canonical)立方体的做法
将一个任意的长方体,转换为一个标准的正方体。
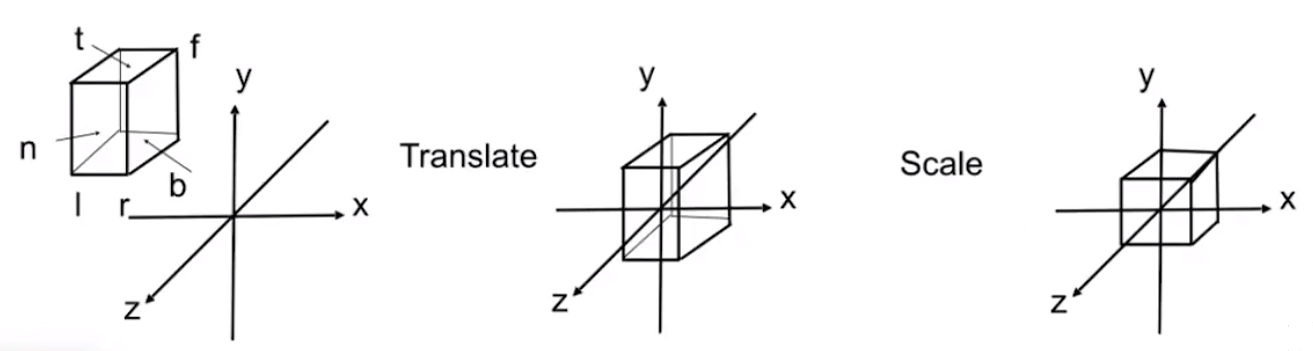
- 把长方体定义成一个 x,y,z 坐标上的范围 x:[l,r],y:[b,t],z:[f,n]
Cube=[lr]×[bt]×[fn]
![image-20201231113534193]()
Mortho′=⎣⎢⎢⎢⎡100001000010−2r+l−2t+b−2n+f1⎦⎥⎥⎥⎤⋅Mortho
Mortho′′=⎣⎢⎢⎢⎡r−l20000t−b20000n−f200001⎦⎥⎥⎥⎤⋅Mortho′
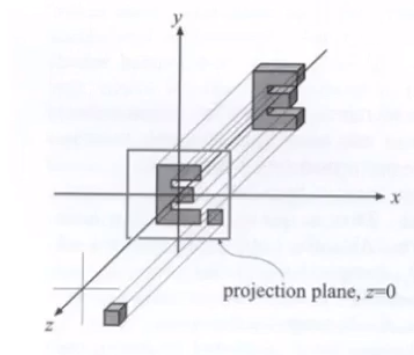
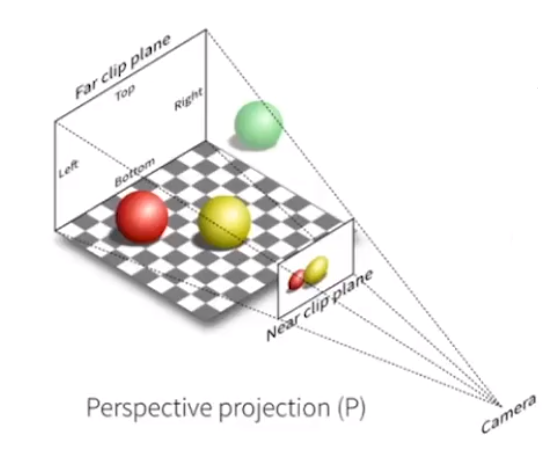
# 透视(Perspective)投影
![image-20201228212755325]()
- 如何表示透视投影下的坐标点:任意三维坐标都可以转为(xz,yz,z2,z!=0)
- 远处的物体,投影到近处以后,大小会随着 Z 的变化而变化 (1,0,0,1)=(2,0,0,2)
(x,y,z,1)→(kx,ky,kz,k!=0)→(xz,yz,z2,z!=0)
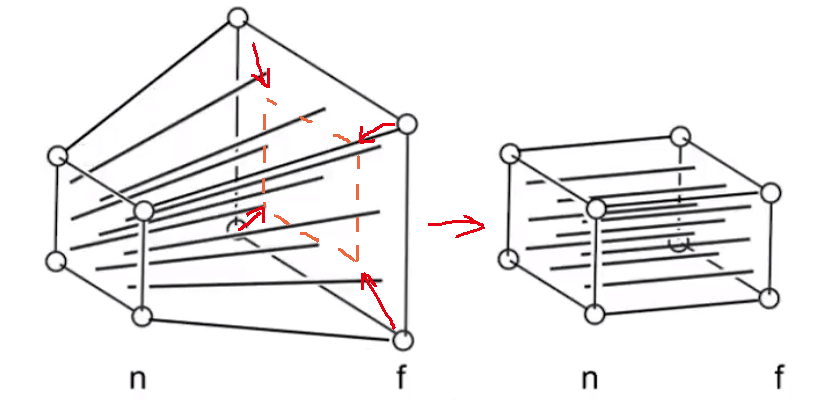
# 透视投影则更像是一个四棱台:
对透视投影通常可以看作是把远平面变换成近屏幕的大小,在对其做正交投影
- 挤压的两个特性:
- 远平面的挤压,不会修改 z 的值。
- 远平面的中心点在挤压和不挤压,都位于远平面的中心。
![image-20201231160609949]()
![image-20201231161327352]()
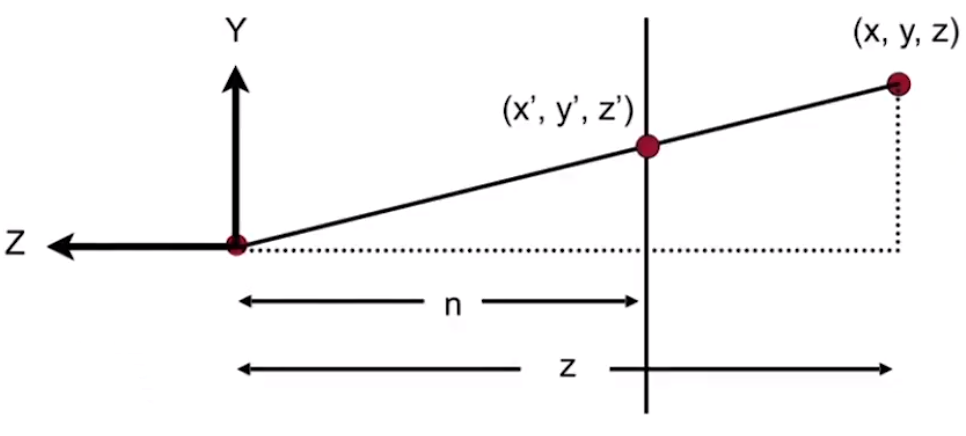
y′=zny,x′=znx
⎝⎜⎜⎜⎛xyz1⎠⎟⎟⎟⎞⟹⎝⎜⎜⎜⎛znxznyunknow1⎠⎟⎟⎟⎞==⎝⎜⎜⎜⎛nxnyunknowz⎠⎟⎟⎟⎞
Mpersp−>ortho⋅⎝⎜⎜⎜⎛xyz1⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛nxnyunknowz⎠⎟⎟⎟⎞→Mpersp−>ortho=⎝⎜⎜⎜⎛n0?00n?000?100?0⎠⎟⎟⎟⎞
设 z = n,⎝⎜⎜⎜⎛xyz1⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛nxnynzn⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛nxnyunknowz⎠⎟⎟⎟⎞⟹unknow=n2,⎝⎜⎜⎜⎛nxnyn2n⎠⎟⎟⎟⎞
n2=(?,?,?,?)⋅⎝⎜⎜⎜⎛xyn1⎠⎟⎟⎟⎞,与x,y无关→(?,?,?,?)=(0,0,?1,?2)→?1n+?2=n2
- 平面的中心点在挤压和不挤压,都位于平面的中心
- 所以 (0,0,n,1)=(0,0,n2,n),近点挤压后依旧是近点
- 所以 (0,0,f,1)=(0,0,f2,f),远点挤压后依旧是远点(这里假设远平面距离f=z)
- 最终的结果就是:先挤压 Mpersp−>ortho 再平移,再缩放 Mortho,最终得到透视投影
?1n+?2=n2,?1f+?2=f2⟹?1=n+f,?2=−nf
最终矩阵结果:Mpresp=MorthoMpersp−>ortho=⎝⎜⎜⎜⎛r−l20000t−b20000n−f200001⎠⎟⎟⎟⎞⎝⎜⎜⎜⎛100001000010−2r+l−2t+b−2n+f1⎠⎟⎟⎟⎞⎝⎜⎜⎜⎛n0000n0000n+f100−nf0⎠⎟⎟⎟⎞